How to support your LGBTQ+ students in the classroom

It’s Pride Month – happy Pride to all of you! In this blog entry, I wanted to share a little about what I’ve learned about supporting gay, transgender, and non-gender-conforming students in the classroom. I write this not as an expert in the social science or history, but simply as a reflective teacher who’s journeyed through the process and the feelings, learned from mistakes, and listened to students along the way – someone who is still learning and hopes to learn from anyone out there reading.

(image credit: glsen.org)

I want to start by recognizing you may be starting this journey a little uncomfortable normalizing different sexual orientations or gender identities. You may not have any close friends or family members who are gay or transgender. It may go against your personal, moral, or religious beliefs. You might see this normalization as excessive political correctness or pandering to people’s confusion and sensitivity. I am not here to argue about any of that – but I will argue that for the sake of the kids, you need to be 100% accepting and caring and put their feelings before yours. It’s a very clear moral imperative and it can save lives. Research consistently supports that LGBTQ youth have higher rates of depression and suicide than their gender-conforming peers. According to the Trevor Project, having even one accepting adult in a gay teen’s life can reduce their suicide risk by 40%. You might be that one accepting adult! Your unconditional support and care can literally save a life, and so as an educator the choice is clear and unambiguous. Support your LGBTQ+ students wholeheartedly – their lives and health depend on it.

What are the best ways to be a supportive ally? What follows are my tips curated from over a decade of listening to my middle-school LGBTQ+ students, again not vetted by science, but mostly vetted by kids.

1. Listen, empathize, and affirm. This is often just what a student needs. Listen without judgment and offer empathy. “I’m happy for you” or “That must be really hard” are simple phrases that go a long way toward making a teen feel heard and comfortable. If you do nothing else in this list, do this.
2. Hang that rainbow flag in your classroom. It’s not virtue signaling and it’s not political. It’s a clear sign to your LGBTQ+ students that they are seen and valued – and a clear sign to the rest of your students that your classroom is a place of acceptance and support for everyone. A flag or a sign invites students to trust you and makes kids feel safer in their own school. I printed out and used a design from GLSEN – you can get a PDF here.
3. Keep confidentiality. If a student is out to you, don’t assume they are out to everyone. Don’t share their sexual orientation or gender identity with others. If there’s a reason you must, ask the teen if it’s ok. Many LGBT teens are open about their identity with some classmates and teachers but not others – it depends on who makes them feel safe.
4. Ask about pronouns – and use a student’s preferred pronouns. If you aren’t sure if a student identifies as a “he” or a “she”, it’s ok to ask what their pronouns are in a respectful way. You could do this as a whole-class icebreaker – “everyone tell me how to pronounce your name, what your pronouns are, and your favorite breakfast food, as in – Ms. DuPriest, she/her, and waffles”. Or, you can approach the student privately and just ask “I see you’re Bailey on my roster, and do you mind if I ask what your pronouns are so I make sure I get it right?” Once you know your student’s pronouns, try hard to use them faithfully, even if they’re different from what you expect. Your student may tell you to use “they/them” pronouns – it’s increasingly common if a teen is in that “Q/Questioning” category of gender identity, or if they are non-binary, pulled neither toward male nor female pronouns, or if they are early in the process of transitioning, or just wanting to show solidarity and support for others – the reasons vary widely, but you don’t need to know the reasons. Just use “they/them” in the same way you would use “she/her” or “he/his”, as a singular pronoun. “Bailey needs a calculator? They can’t find theirs?” – it’s easy enough for you to say and means the world in terms of helping your student feel seen and valued. It may become awkward for you to use gendered phrases you typically use in the classroom, like Young Man and Ma’am, so you’ll have to adapt. It is hard to teach an old dog new tricks, and you’ll mess up from time to time. Just apologize quickly and try to improve, and be patient with yourself.
5. Don’t make assumptions. A teen’s gender expression might be different from their gender identity, so if you’re confused, just ask about the pronouns respectfully and go with that. In other words, you might have a student who looks and dresses very feminine but has a masculine name and tells you they use he/him pronouns – and in this case, use the name the student gives you and the he/him pronouns and be 100% accepting about the way they look and dress. Don’t make any assumptions about their anatomy or chromosomes and don’t ask – it’s none of your business and may have nothing to do with the kid’s actual identity. Each of us is the expert on who we are individually, and this kid is an expert on who they are – go with that.
6. Check with the student before calling home. When you need to communicate with a student’s parents, check with the student first to find out the name and pronouns their parents use. I have worked with kids who aren’t completely “out” to their parents, or who use a different name and set of pronouns with school and friends. Just ask “I need to give your folks a call, are they fine if I use your name and pronouns?” I am always glad I asked.
7. But don’t assume they’re unsafe at home. If a kid isn’t out to their family or doesn’t use their desired pronouns with family, it doesn’t necessarily mean they’re unsafe at home. But it is ok to ask a student if they’re safe and supported at home and if they need anything from you. As always, it’s smart to remind a student that you are a mandatory reporter and if they tell you that they are unsafe at home or school, you will absolutely get help for them.
8. Help make the school bathroom as low-stress as possible for all of your students. For a transgender or non-gender-conforming teen, just going pee can be the most stressful part of their day, not knowing if the toilet they’re going to use is acceptable, if kids will look at them weird or harass them once they’re in there, etc. At the bare minimum, just support your students going to the bathroom wherever they feel most comfortable. Some schools provide solo gender-neutral bathrooms for students to use when needed, but these aren’t available everywhere. You might find that some students walk all the way across the building to find the bathroom they know they are safe using. It might be especially stressful if a student is at an event like a football game or a dance when the usual bathrooms aren’t available. Provide supervision outside of the bathrooms, be aware of who’s going in and out, and communicate with your students privately about if their bathroom situation is ok and comfortable or if they’d like a different solution.
9. Be an outspoken advocate and an ally. If you are ready to openly advocate for acceptance and be more of a direct ally, I suggest giving a short presentation to all of your students about how to be a good friend to their LGBTQ peers and why it’s important. This is one that I use on National Coming Out Day, with fewer and shorter bullet points so it’s a little more kid-friendly. 🙂 I also suggest you download GLSEN’s Safe Space Kit and go over it yourself, as it has great tips for being an ally to your LGBTQ+ kids. Consider following Brett Bigham on Twitter, who consistently shares helpful tips on supporting a positive culture for LGBT kids and teachers.
10. Have high expectations, and know that kids need to feel their feelings. LGBTQ+ kids are not delicate snowflakes, and you can and should hold them to high academic expectations as with any kid! Know that, as with any teen, they’re going to be in their feelings sometimes and school won’t be the top priority in their minds. Use good pedagogy for adolescents – allow them to write, to reflect, to speak, to create, and to do hard things, achieve genuinely, and share their work. Don’t lower the expectations to protect them – it won’t serve you or them well!

What other tips and suggestions do you have for making your classroom and school welcoming and inclusive yet also challenging and fulfilling? What have you learned from your LGBTQ+ kids? Thanks for sharing!

Hybrid Teaching.. week 3

I didn’t fully appreciate how exhausting hybrid teaching would be until I tried it… but friends, it’s exhausting. It’s beyond first-week-teacher-tired. I’ve never seen anything like it.

It’s been really stressful and slow, and the planning load is extremely heavy, and the constant anxiety from the threat of COVID-19 just nags at me all day long.

It’s also been joyful. The students that come to school in-person are truly happy to be there and are enjoying being at school. I get to teach things that I enjoy, to kids that are happy to learn from me, and they constantly ask questions and beg for snacks and demand computer help and I can see why it’s so exhausting for parents to manage online learning… and I’m happy to be that person that can make this a little easier on everybody for a little while. The person that can make the kids smile and help them explore new ideas, take them to the park and play games.

So here’s what we’ve been up to in the last few weeks.

My schedule looks like this now:

• Morning: 6th grade math, fully remote

• Morning: 7th grade math, fully remote

• Lunch

• Afternoon: Venture Project, hybrid. This means I have half of my class doing a live lesson (about 7 in the classroom and 4 or so on the Zoom at the same time), and half of the class working independently. Group A gets a live lesson Mon/Wed. Group B gets a live lesson Tue/Thu.

• Fridays are fully asynchronous and teachers have office hours, meetings, and planning time.

The planning load for the afternoon class is so hard. Twice a week, I have to do a boat-ton of planning. I need a 3-hour synchronous lesson that will work with both kids in the room and kids on the zoom, and I need a 2-hour independent lesson, right at the correct level of difficulty so it’s relevant and interesting and doesn’t feel like “busy work” but also doesn’t require a lot of intervention from me. My Sunday and Tuesday nights have been running really late, working until midnight or 1am trying to pull those lessons together. I also need two math lessons every day so I can’t neglect those.

I always structure my venture projects this way, though. This quarter my venture topic is “Art Enhanced by Technology”. We are exploring how modern technology can make art more meaningful, immersive, beautiful, and interactive. Venture projects follow the design cycle over the course of a quarter. The first phase is Empathize, and I take that job seriously. So we profile different artists, do research, get feedback from each other, and I teach the students the content skills they’ll need to be successful in the venture. In this case, it was a brief blast of creative coding, Arduino, 3D printing, laser-cutting, and virtual reality. It’s been really fun. Just a lot of work.

Socially-distant VR lessons. Headsets are, of course, not shared, and yes you can wear a face mask and a VR HMD at the same time. If someone else needs them, we clean with disinfectant and let the headsets sit unused for a few days before they’re used by another classmate.

The students really enjoyed using Neopixels and learning about Arduino. I made kits for the Zoom students so they could join in from home.

The planning load tends to get easier as I get farther into a venture, because the load transfers from me to the students. They’re getting ready to put together project pitches to create their own technology-enhanced art and communicate as an artist.

Unfortunately, community spread of COVID is so high that our brief time learning in person will be ending soon. We decided to go fully remote after Thanksgiving and give our community time to flatten the curve – and we really hope they do. We do our level best at school, keeping groups small, being vigilant about masks, hygiene, health screening and quarantining when necessary. It’s exhausting but it IS possible to create an environment in which you don’t have outbreaks… provided you don’t have too much spread in your community. We’re getting to a point where there is so much spread we can’t reasonably promise to be safe.

It’s been good while it lasted. But I will be a little glad to go back to the remote schedule – I know the students don’t love it, but I do get more sleep that way and my personal anxiety is not so high.

Stay safe out there, everyone.

We Actually Reimagined Education During the Pandemic: One School’s Story

I have been wanting to blog about the biggest changes I’ve been part of since the beginning of the Covid-19 Pandemic. My school seized on the opportunity presented by the big disruption of school…. and we reinvented the school. We threw out old systems that weren’t working for us and created something new – systems that would work for us if we were still learning remotely, but could be made even better and more powerful when we went back to full in-person school. I am grateful that Dr. Byron McClure encouraged me and my school leader to put the words down, and he hosted our blog. It’s linked here! Lessons for SEL Blog

Thank you, Byron, for your encouragement and enthusiasm! And thank you all for reading. Let me know if you have comments! You can find me on Twitter: @DuPriestMath.

Online Teaching weeks 4-5

I’ve made it a month into full-online teaching! I’ve got my 6th grade math class, 7th grade math class, and grades 7-9 venture class every Monday-Thursday. Friday is a day for staff development and asynchronous work. Here’s the report for these weeks and any other pro tips I can share.

Math:

I am going to jinx it, but I think I’m hitting my groove in math. I have never really taught 6th grade math before, and I’m rusty on 7th grade math, but I’m finding my way. I have found that if I take the workshop-style problems I normally would have given kids in class on paper, and convert them to Desmos activities, the lessons flow pretty well and most kids are engaged and active. I make Desmos activities for literally everything. I’m not the most advanced user of the Activity Builder, but these allow me to guide the students, fix problems and coach them in realtime, see everybody’s work, curate samples and share them out with the class… it’s getting there. Today I did an activity and I could tell some kids were flowing well with it and others were really stuck. I asked the class if they were ready for a hint, but a few students yelled loudly “No hints! I want to figure it out myself!” So then I tried a new teacher move, and I told the students if they wanted hints, to send me a private message in the chat, and I would invite them into a breakout room and I’d give them hints there. 5 students sent me messages, and I pulled them into a breakout room and gave them the hints, and we went back to the main room.  It was super cool to see that students didn’t want hints and wanted to figure it out on their own, and the students that came to the breakout room were grateful.

My three teaching tools I use over and over again: I create activities in Desmos and pace them so we can discuss problems every few slides; I pause, run over to my laptop, train the camera on my whiteboard and give a few quick notes and examples; I assign homework and quizzes in Khan Academy. I assign work twice a week, always with 2 days to complete assignments. I have never gotten a good response if homework is due the next day, and some kids have busy lives and can’t rearrange everything to accommodate last-minute homework.

Here are some of the Desmos activities we did the past two weeks:

Fraction division: “No Matter How You Slice It” activity

Fraction Problem Solving: Food Problems adapted from Robert Kaplinsky’s site

Decimal Addition and Subtraction (6th grade): The students were pretty comfortable adding and subtracting with money, so I used this activity to introduce them to adding and subtracting with more than 2 places past the decimal. After every slide we stopped, took some notes, and had a quick discussion.

Multiplying Decimals Card Sort (6th grade): Before the card sort, I gave the kids some notes showing them fraction/decimal multiplication equivalents. For example, 3/10 x 7 = 21/10 = 2 1/10.  This means that 0.3 x 7 = 2.1  because 0.3 is 3/10 and 2.1 is 2 1/10.  We did a few examples like that and then the students did the card sort. I paused every so often and let a student explain a match they made and why. The 2nd and 3rd slides are a warmup before we start multiplying multi-digit decimals.

Adding Integers (7th grade): I used this as the first lesson on a unit about rational numbers. The students really enjoyed it. I paced it so I opened up 2 or 3 slides at a time, and we would have a discussion and share work after each group of slides.

Adding Rational Numbers and Intro to Subtraction (7th grade): I adapted a lesson about bank statements from Illustrative Mathematics to introduce adding positive and negative decimals to the students. We introduced integer subtraction and subtracting negatives. The “bank statement” part of the lesson was very challenging, because of the many concepts and skills packed into it. Decimal arithmetic, understanding of where these numbers go on the number line, attention to precision. A gap in any of these could cause a student’s balance sheet to turn into a disaster quickly.

Venture:

I’ll just quickly add that in my venture class, the students are now doing their project pitches, and although I’m nervous about running into a time crunch with the end of the quarter…. I love the project pitches they’ve given. They are all doing a project about something they already love and enjoy, and tying it into the theme of “The Impact of the Internet”. One student will be making an informational webpage about chihuahuas. Another student will be making a dog feeder from a Raspberry Pi. Another will be publishing history videos on a YouTube channel. I am cautiously hopeful that they will learn and love their projects and get a lot out of this weird quarter of school.

Each day I’ve started to add creative writing activities to Advisory and that’s been more fun than I expected. I haven’t done creative writing in a long time and I’ve even gotten sucked into it. The topics here are a little grown-up for my students, so I adapt them a little, but Jane McGonigal is a futurist I follow on Twitter and she published this “game” which is a creative thought-experiment about disaster scenarios for the information age. They’ve provoked really great discussion during a time when kids’ cameras are usually off and they’re silent, so since the kids have found this engaging, I’m sharing with you:

The First Five Minutes of the Future

Try it with your advisory students – do a 5-10 minute quickwrite, then make breakout rooms and share out what you wrote and have a discussion afterward with Jane’s followup discussion points on the web link. The kids will enjoy it and so will you.

Pro Tips:

• Not really a tip so much as a life skill… you gain nothing from being grumpy with the kids right now, and they gain nothing. So just be kind. If a kid has their camera off and isn’t participating, check in on them. Say “I haven’t seen you or heard from you and just wanted to check in. Do you need any help?” And just keep asking. Wave goodbye with a smile every class. Here’s a pro tip I learned in pre-teacher service that I still use. Tell your class, every day, that they’re your favorite class and you really enjoy them. Say it for a week or two and it’ll be true, I swear.
• Get up and move. You can’t do remote teaching from your chair all day. You normally move when you teach. Shift to a standing desk or angle your camera so you can draw on a real whiteboard and stand up. It’ll help, I promise. If nothing else, you’ll be more animated and enjoy presenting more.
• I’m going to put it out there that I am very much warming up to using Khan Academy for homework and I think I’m going to use it all year. What a gift to not have to grade homework or quizzes…. I can spend more time analyzing what they know and don’t know, and less time just marking up papers. 9/10 other than a few minor complaints it is very much recommended.
• Get blue-light filtering glasses. It has made a huge difference… I used to suffer from migraines every week and I have only had one mild headache since I got the glasses. I got them for my kids too. Essential for remote learning!
• Celebrate the kids’ pets. You might as well, you can’t have them at school. Sing awkward birthday songs. Change your background. Play lobby music. Give silly attendance prompts. If doing stuff other than math content increases engagement…. then yes, do that.
• One  last pro tip: If you’re teaching on a PC and not a chromebook, you can install Snap Camera and use that as your camera in Zoom. Snap Camera lets you apply filters, so you can teach with mouse ears or rainbow hair or looking like a potato. If engagement is suffering then definitely get Snap Camera.

That’s it, have fun out there everyone.

 

 

 

Online Teaching Week 2-3!

I don’t have a lot of exciting lessons to report, but I wanted to share out some tips, tricks, and general observations from online teaching now that I’m into the flow of it a little.

In math 6 and math 7, I taught the same review unit for both – fraction operations. I thought it would move faster with my math 7 crew, but I found as we got into it that they needed the review just as much as the 6th graders. The curricula diverge after this week, but it was nice to reuse the same lesson plans for a brief moment. 🙂

I continued to use Desmos as my main teaching tool. When we were working on multiplying fractions, I did try an activity with Jamboard where I put the students into breakout rooms and assigned them tasks that I adapted from the Connected Math Bits and Pieces II textbook. I thought I modeled the activity well and set it up for success, but when the students were put into breakout rooms, they got quiet, refused to talk to each other, scribbled on the jamboard and then erased each other’s scribbles and really didn’t engage with the math. Frustrating. I stopped the activity and went back to individual tasks for the moment. Flash cards still work ok in breakout rooms, but the harder problem-solving is not something I can have them do in groups yet.  Here’s the jamboard in case you want to use it. Maybe you’ll have better luck or suggestions for virtual group work?

https://jamboard.google.com/d/11Zhqx6KNwXc1r6HlOsXSGaon5EowGQLjC49tJb2OWao/viewer?f=0 

I stepped back after that activity and I changed strategies. I taught the students the algorithm for multiplying fractions (numerator x numerator, denominator x denominator, then simplify) and gave them some Desmos tasks to evaluate expressions using the algorithm and then explain why it worked using a drawing. This led to a pretty good discussion and better quality of work from the kids.

https://teacher.desmos.com/activitybuilder/custom/5f5708548c04720cbb8adcf8

After every 2 slides, I would pause and give the students a small amount of notes – multiplying fractions, multiplying a fraction x a mixed number, then multiplying two mixed numbers.

We used this Desmos activity for division expressions involving unit fractions. It was a good activity and again, we had high engagement and a good discussion.

https://teacher.desmos.com/activitybuilder/custom/5f585985ee812a34cbda5b06

Now I am at a point where I want to give the students a quiz to see how their fraction operations are coming along. I have a Desmos “quiz” prepared and also have curated the Khan Academy unit quizzes covering the same topics. I think I’ll assign the Khan quiz in class, but if students need to do a redo, I’ll let them to retake using the Desmos quiz.  We’ll give it a try!

One more note about teaching math: I wish I could find it now, but back in August I saw some tweets from another math teacher where she tried giving notes using the Zoom whiteboard tool, and then using a physical whiteboard with a camera trained on her, and when she asked her students what they preferred they said they liked the physical whiteboard better. I decided to try this too, and I like it a lot. If nothing else, it gets me moving – it’s amazing how much I even miss that part of teaching, the standing and the moving! So I have my desktop computer on my normal desk, and then I have a small podium where I put my laptop facing the whiteboard. I have my laptop join the Zoom call along with the students. If I want to give notes, I mute the desktop, run over to the laptop, unmute it, and write on the whiteboard. I take photos of the whiteboard with my phone so I can post notes later for students that need the notes for their accommodations.

For advisory and venture, we finally finished playing everyone’s kahoot quizzes, and I started on a lesson on identity that I adapted from tolerance.org.  I think the lesson is supposed to be used for teachers to reflect on their own identity… but it was useful for students and actually generated good discussion… and good discussion is SO hard to find in online teaching! The kids asked thoughtful questions and mainly wanted to know about vocabulary terms… what is ethnicity? What is socioeconomic status? And they reflected a little on times when they took their identity for granted and when they found they had to adapt because they were not in a dominant identity group. It was good.

Here are the slides I used.

Identity Presentation

We continued with the “Empathize” phase of the design process – I curated lots of articles, videos, and other resources for us to discuss together, and we started brainstorming potential design project ideas. I’ve been able to wrangle up a few guest speakers for my venture class that I’m pretty excited about – and this is one area in which remote teaching really has an advantage. It’s a lot easier than it used to be to arrange for a career speaker for my kids on short notice. If they’re available and ok with me sending a zoom link, we can have a career talk in class. No travel, no visitor badge and check-in system, no need to arrange for equipment to be transported – just a zoom link. I have an artificial intelligence specialist from Skype-a-Scientist coming next week, a data analytics specialist from Kyruus who will talk with the students about data privacy and healthcare data, and Des from DesFit, who will talk with the students about the life of an internet influencer. Fun! I’ve also taught the kids a little HTML, CSS, and Javascript coding and am going to check out Raspberry Pi kits to a few students who want one.

Other random tips about remote teaching:

• I have one of those Ring Lights, and I definitely prefer it to the overhead lights in my basement.
• I got a small standing desk, and at lunch I pick up my monitor and keyboard and stand for the rest of the afternoon. It helps SO MUCH.
• I have continued to start each class with broadway show tunes and a silly attendance prompt, and these routines have become really important to me and the kids.
• I ordered some blue light filtering glasses and I also turn my monitor to Night Light mode during the day. It has actually helped with headaches a lot – I can’t believe I never tried this before.
• If kids have pets on screen, of course we acknowledge them and enjoy them. I appreciate something that makes the kids turn on their cameras and interact with each other… and pets do the trick sometimes.
• I am still up late most nights and work some pretty long hours and don’t get out of the house much. Getting the content organized is a small part of the teaching challenge… organizing it so it flows online takes the most time. I feel like I have to be hyper-organized with everything. When I teach in person, sometimes I don’t even write lesson plans, I just have a rough sketch of what I’m going to do and I march in and wing it. I do not feel like I can do that right now. In this respect I feel a lot like a first-year teacher again.
• I have 5 minutes of passing period between my morning remote classes and IT IS NOT ENOUGH!! I show up late to my second class more often than I’m comfortable with! But sometimes I have a kid in that first class who needs just a couple more minutes to figure out how to attach the file, take the screen shot, find their late homework, whatever… and it’s not like I can just go find them at lunch, you know?  I wish I had a little more time at the end of class for those last-minute things.
• I’m finding ways to make remote teaching work and am pretty proud of what we’ve been able to accomplish in spite of the challenging circumstances… but I ache to just be back in the classroom with actual people.

Online Teaching Week 1

It’s now Tuesday September 1, and I’ve been teaching fully online for a week. My class is a competency-based, Project-based learning school, and this is only our third year even existing as a school, so it’s been completely novel preparing to do school this way.

I teach two classes of middle school math in the morning, and then our venture block in the afternoon. Venture projects look a little more traditional in the beginning, but as we progress through the class, it becomes more individualized and problem-based and eventually we fold in the design process and turn it into a project. My venture class has a theme of “The Internet Age”. We’re exploring the technical and social/cultural impacts of the internet, and then each kid will be responsible for coming up with a problem statement and doing a design project. I love the topic and am really enjoying teaching it so far.

I just wanted to throw out a few thoughts on things that are working and things that are challenges so far, in case it’s helpful to anybody else.

It’s HARD work. I am up late every night planning, re-configuring lessons I used to have and writing new lessons. Part of this is my prep load and part of it is that even the stuff I do know how to teach, I need to revisit all of it.

It’s exhausting. I am having a hard time telling whether first-week-teacher-tired is really that much worse than previous years. I think it *feels* more exhausting because you just never get away from it. You never get in your car and go home. I’m just at work all the time.

It’s not as soul-crushing as I thought it would be. I enjoy seeing the kids. I can still listen to their funny stories, I love seeing their pets, I love our little routines that help us get to know each other. I start each Zoom session with music, usually Broadway show tunes, and I change my background so it matches the music, and the kids guess what it is. I change up the daily attendance prompt every day so every kid gets a chance to speak and tell me more about them. I dedicate a little time twice a week for me and the kids to do a little tech troubleshooting together, and we are learning together the best practices for managing all the tools.

I have a short chunk of advisory time with my students, and for the first week, I decided to dedicate that time for us to get to know each other. So I had each student write a 10-question Kahoot quiz about themselves, and we take a couple of quizzes every day. To me it feels like a lot of Kahoot, but I think the kids love it – they ask about it as soon as they log in. “Are we doing another Kahoot? Can we do mine?” They’re freshmen in high school but soooo excited about sharing and playing their Kahoot quizzes.

For math, my favorite tool is Desmos. I feel like I have a better idea where the kids are in math than I even do when teaching live. I’ve assigned work in Deltamath and Khan Academy and I’ve also assigned Desmos activities, and with the Desmos activities I can look at the kids’ sketches and what they wrote and I know whether they understand or not. With the other tools, I see what they got wrong, but it’s really tough to tell whether or not they get a concept.

I look for problems in the old Connected Math Project textbooks, the Illustrative Math textbooks, Robert Kaplinsky’s problems, Geoff Krall’s Emergent Math curriculum, and wherever else I can find good activities. I put them onto Desmos slides, make any images into sketch-area backgrounds, add a block to enter a math formula and an explanation, and voila, it’s an awesome formative assessment, individual activity, or group activity. Here are a few of the activities I adapted. They’re for 6th grade math.

Sharing Pizza

Comparing Fractions with Grids

Dividing Land

For venture, I have decided I love Mural. We do a lot of reading and discussion – and discussions are so, so hard in this virtual medium. SO HARD. Kids are so shy, they turn cameras off, they type one or two word responses in the chat, they say the bare minimum and then turn off the microphones. But if we read an article and then I give them a canvas with an unlimited supply of sticky notes, they have a lot to say. Mural has a timer so the kids have their timer in front of them at all times, and it has anonymous voting tools – so at the end of a sticky note session, the students can vote on their favorite discussion points and then they’re displayed for everyone and the conversation can actually get going.

I created a lesson on the impact of the personalized news feed on how you view the world. I really liked how Mural helped to facilitate this discussion – when we processed what we learned the next day, it was apparent the big ideas of the lesson were still percolating. In the Mural, we first read together the article in the top-left about Mark Zuckerberg’s announcement that Facebook would be changing its News Feed algorithm – and then I taught a little bit about the events in Kenosha Wisconsin – just factual information – and I had the kids split into two groups, and one group read conservative analysis about the events and one group read liberal analysis. I asked the students to imagine what they would think about the killing and the protests in Kenosha if the majority of their news feed was like the articles they read.

Here are the links to the lesson.

Personalized News Feed slide presentation

Personalized News Feed Mural

 

I do random breakout rooms. Setting up premade breakout rooms is really time consuming, but I will do it when the need comes up. So far my strategy is to just apologize for making it random and remind the kids to tell each other their names and about the basic norms of group work. Some breakout rooms work really well (I had the 6th graders do flash cards in groups of 3, and it was awesome, and the 9th graders played win/lose/or draw, and that was great) and some are completely silent and unproductive, so I am still working on how to find the magic sauce that makes breakout rooms successful more often than not.

In general, the hardest part of this teaching is student engagement. It is really easy for the kids to turn off the camera and mic and just disappear. I don’t shame them for it, but it’s awfully hard to feel like you’re teaching into a void. So occasionally I will prompt them to engage “Can you still hear me? Is this thing on? Give me a quick thumbs-up or tell me your favorite sandwich in the chat so I know you can see my screen.”  Or “On a scale of 1-5, 5 being the MOST confused, how confused are you right now? Hold up fingers or type in the chat.”  Desmos and Mural activities are so far the best ones to foster engagement, but I hope to add to the toolbox as the quarter goes on.

 

That’s pretty much what I know. Soldier on, everyone. We can do this.

 

My experiences with White Supremacy… you know it as NIMBYism

I’ve been sitting back and reading a lot in the current cultural whirlwind and rejuvenation of Black Lives Matter. The movement has come a long way. The tide is turning. I feel cautious about real change happening because I’ve seen how powerful inertia can be… and if we’re going to see a true dismantling of systemic racism, it means as a society we need to open ourselves up to being uncomfortable. And unfortunately, I do not think white America is ready for that. We need to take a hard look at how white supremacy shows up in our daily lives… it’s very obvious in the context of police brutality, but we all live in it, baste in it daily without recognizing it for what it is.

To see how white supremacy manifests itself as intertia, I want to take a look at just one aspect of racism in education – school boundaries.

I’m going to show you some statistics from four schools in my city. These schools are just a few miles from each other. It’s not a huge town. The distance between School 2 and School 3 is 1.5 miles.

	% Free/ Reduced Lunch	% Hispanic / Latino	% Proficient Math	% Proficient ELA
School 1	74	69	14	23
School 2	89	57	20	27
School 3	24	4	62	68
School 4	35	19	59	63

My town has a very small Black community but a sizable Hispanic / Latino community, and you see the racial component of this when I break out the data this way. In the north part of town, it sure looks like the school boundaries were drawn to cluster the free/reduced lunch kids and the Latino kids into School 1 and School 2. There is some white flight from school 1 and school 2 as well… some students who live in the boundaries of those schools choice into other schools in the district or go to charter schools. Even so, it is really remarkable that the boundaries are drawn this way. It’s also segregation. It’s not equitable or fair. It really wouldn’t be that hard to change, just move the boundaries literally a few blocks in one direction or another. I can tell you from talking with friends who have taught in schools 1&2 and their feeder middle schools and high schools, that those schools are really hard to teach in. You have to develop a much bigger toolkit to work there. It can be frustrating and draining and stressful. My only experience in that realm is teaching the grade-level and remedial math classes in my own middle school for a while. They were exhausting. It was so hard to cluster all of the kids who didn’t like school and already weren’t successful with math in the same classroom and try to help them grow. For a few years we de-tracked our math classes, breaking down the “honors vs. grade-level” paradigm and creating heterogeneous classes, and it was SO much better. The mixed classes were way better to teach, kids made better growth and the teachers enjoyed our jobs more. Slowly though, the old paradigm came back and we started splitting the classes into “honors vs. grade-level” again. I think you need a rich toolkit to teach heterogeneous classes, and it keeps you on your toes more, but it is overall a more rewarding experience. I did some reading on the benefits of integrating schools and I am convinced it’s something we need to do. I don’t understand why we keep drifting back into separating kids. Well, I do though. It’s comfortable. “Comfortable” is at the heart of this conversation, and to use a loaded term, “Comfortable” is at the center of white supremacy.

Around 2015, my district had some boundary-redrawing discussions as we prepared to create a few new schools. I wasn’t on the boundary-creation committee, but I attended a few meetings. I wish I had said more then. I looked up the information you see above because I wanted to have some background knowledge, and I was surprised and shocked at the level of segregation in my generally affluent, “friendly”, high performing district and town. I went to the meetings prepared to push on this – to challenge the school board and leadership team to take the opportunity to break down some of this segregation and have mixed schools. But when the meetings started, they opened with several proposals already written that made zero changes to the parts of town that, in my mind, needed them – and the comments were pretty bland, the mood was not at all contentious, and I got quiet instead of stirring things up. I regret that now. We just kept the school boundaries mostly the same and the numbers you see in the table are pretty much the same ones from 2015. A missed opportunity.

Also in 2015, a new housing development was proposed adjacent to my neighborhood. We had this oddly-shaped triangular lot next to our neighborhood ever since we moved in, right on a busy intersection, full of weeds. We knew it would get developed someday and were happy when the proposed development was a nice neighborhood – a Habitat for Humanity community. At least it wouldn’t be a KFC or something, right? I remembered my neighbors were NOT on board with this and at first they convinced me to oppose it too, but by the time the community meetings came around in 2015 I had decided to support it. Our town desperately needs more affordable housing. My dad volunteers with Habitat and speaks fondly of how rewarding it is to see a neighborhood get new life and a new sense of community when Habitat homes are built. That the kids who live there actually have their own rooms and a quiet place to study, and their grades improve. The families get financial security for maybe the first time ever. Plus, we have a Geometry and Construction program at two schools in town, and our local high schoolers actually build the homes. This was an important cause to get behind.

 

An artists’ visualization of the Habitat community before it was built. Super cute! Image credit from Namaste Solar who partnered with Habitat for renewable energy.

I went to a community meeting and was absolutely blown away by how awful my neighbors were about this “low income” housing community. It was embarrassing and shocking. Many of my neighbors made comments about the traffic and the density and how they would lose their views (over an empty lot??). The pearl-clutching over these inconveniences were out of proportion to the actual suffering we would endure because of a housing development going up. Some actually came out and said they were concerned about the “wrong kind of people” moving into the neighborhood. That it would attract crime. That it would strain the schools and “those people’s kids” would cut through our neighborhood to get to school. That our school’s quality would decrease. That our property values would go down. Now we don’t exactly live in a wealthy gated community. Our homes are really, really average homes in a really average part of town and I couldn’t believe the sense of entitlement and elitism I saw at the community meeting. Wow. I was one of two people that stood up and spoke in favor of the project. The other person was the Geometry and Construction teacher whose students would be building the homes. I think he was shocked too at how unwelcoming people would be to this project that he and his students had invested so much into.

This is a snippet I found online from the meeting. The full document with notes from all the community meetings is here. https://www.fcgov.com/developmentreview/pdf/harmony_cottages_type1_files.pdf?1558477510

The first comment is my part. The next question came from a neighbor. I don’t even know which one. So many of them said the same thing.

“Everyone loves Habitat, but not here.”  Over and over. “We have no objection to Habitat for Humanity, but why in our neighborhood?”  The traffic, the noise, omg the low income people living one block away and the crime and their kids interacting with our kids and going to the same school…..  It was horrifying.  I understood why our school board and district leadership don’t really put their whole selves into integrating our district schools over income and race. They don’t want to have meetings like this. I don’t blame them, but we shouldn’t keep avoiding this. Avoiding the backlash is why inertia sets in. Why we settle into what’s comfortable, just separating people according to our natural divisions of class and race and just not fight it. But segregated schools lead to inequities all the way down the line, we know this, we know it’s wrong and the legality is sketchy and we do this anyway – because it’s comfortable, and convenient. Comfortable and convenient are the hallmarks of white supremacy.

The Habitat community did get approved eventually. There are several houses built now and families living in them. One of my current students will be getting one of those homes with her mom. When we had online learning during spring 2020, she had to attend zoom meetings on a phone from her bathroom to get some privacy. Won’t that be amazing when she has a house? The neighborhood is super cute and we like watching it come together. My grumpy neighbors are still mad about it.

At some point in this timeframe, I was listening to the radio and a rerun of This American Life came on, and it was Nikole Hannah-Jones’ special about her experience with school integration. It was riveting. Especially the parts in the broadcast about the parent meeting regarding school integration. That meeting could have easily been in my town, my neighborhood. Here’s the broadcast.
https://www.thisamericanlife.org/562/the-problem-we-all-live-with-part-one

I felt vindicated listening to the broadcast, I felt understood – my experience with my embarrassing, classist, NIMBYist neighbors was way more universal than I imagined. The wild, mind-blowing thing is that school integration, and neighborhood integration, are helpful. It’s beneficial to kids of all races and backgrounds. It makes for a richer teaching experience for the teachers. It really wouldn’t be that hard to do in my own town – really, really easy. Except for the discomfort of white people.

I realized in processing societal integration and the pushback to it, that a lot of white supremacy just looks like comfort. Anything that makes us have to put a little more effort into our lives – wait an extra minute to make that turn, or listen to the families from a different race and class over the fence, or put a little more effort into including people – and we crumble. We’ll cram into yoga studios and train for half-marathons and stay all weekend at our kids’ softball tournaments, but if we are forced to make tiny changes to our everyday lives to accommodate other people we perceive as different… we fall apart, and we do so loudly and violently.

We need to seize this moment and make positive moves toward racial equality. But to do this, we – white people – need to start letting our communities know about the changes we want to see. I really want to see my own school district develop some courage around racial integration and I want my white community to not fight it so hard. This isn’t going to happen just from my wishing it so. I need to speak up for it, and patiently advocate for it, and celebrate small steps of progress, and be prepared for backlash, because it’ll come. And YOU need to speak up for it. It’ll take white people in numbers to do this, but if we are serious about making a fairer, more just, more equitable society, school and neighborhood integration have to happen.

Teaching a DIY Solar Charger Project, remotely

Along with my math preps, I also taught a venture-project class this quarter. I had planned a very hands-on project and purchased a LOT of supplies for the students to make solar lamps, solar chargers, and solar cars. When we shifted to remote learning, I decided to try and make this project run, if a little scaled down. I split the kids up into groups, and a group of 6 middle-schoolers got assigned to be on the Solar Charger team. I have never built this project with kids before and have spent the past few years trying to get the electrical design nailed down. But I really wanted to do this project. All of our ventures focus on community needs, and we’ve worked with the FoCo Cafe and Homeward Alliance over the years to bring donations to the homeless. They’ve mentioned before how awesome solar chargers would be. At the shelters, people often crowd around outlets so they can charge phones. For people experiencing homelessness, if they have a phone, it’s a crucial communication tool- a connection to the world. But if you don’t have a permanent place to live, having access to electricity can be a challenge.

Over the past year, I settled on a design for a solar charger using 18650 batteries (these can sometimes be found in laptops and vape pens, but I bought them off eBay) and a TP4056 charging circuit. It’s not a perfect solar charger. If you plug the circuit into the wall using the micro-usb port, the batteries hold enough charge to charge your phone more than once. Although the batteries say they’re 3.7v, they can be charged up to 4.2v with a wall charger. However, if you charge the batteries using the solar panels, it seems the current never quite gets high enough to charge the batteries that last little amount. I can get up to 3.95 or 4.05 volts, which is enough to charge a phone about 2/3 of the way. But after experimenting with a bunch of different charging solutions I determined that for a reasonable price, this is as good as we can do for now.

I worked out the electronics with the help of student testers over about 3 school years, but I never had a mechanical case I liked. In the past, I used upcycled food containers, and they were flimsy.

When I met with students this year in our “charger team” meetings, our first task was to design a sturdy case for the solar charger. We discovered you can collaborate in Tinkercad and it turned out to be a great solution! We all logged onto the same Zoom meeting, and then I created a Tinkercad project and clicked the Collaborate button to share it with everyone.

It’s amazing. You can all edit the same project at the same time. And with this group of kids, it turned out ok. We downloaded a couple of charging-port holders from Thingiverse and embedded them into a box, with some walls to hold the battery pack in place. The kids worked with rulers and measured battery packs and solar panels, and we updated the measurements in the file. Our first design had the voltage-in (micro USB) and voltage-out (USB-A) ports on opposite sides, with a flat lid.

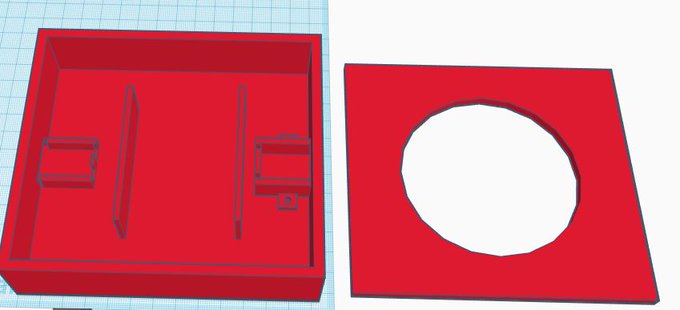
This was iteration 1. The box took a really long time to print. I printed one at home, and showed them how it turned out at our next meeting. I asked the kids if we could make it a little smaller to save filament. So we moved both charging ports to the same side, and made the box exactly the same size as two solar panels side by side – and only slightly taller than the battery pack. I printed multiple copies of this version and then had a meetup with the kids to give them cases and electronics to try and build a solar charger. I parked at the school, and the kids pulled up with their parents where I handed off a bag of parts, soldering irons, and other tools.

A masked-up, hands-free supply exchange so we can do a makerspace project.

The students worked with iteration 2, and each one in the team built a charger.  I shared video instructions for creating the charger, and we had a zoom session that was a “learn-to-solder” lesson. The next time we met on zoom, they reported back that overall they liked the design, but the slots for the charging circuits needed a little re-designing. They wanted the slots overall wider, with a lip to hold the circuits in place. We made changes together in Tinkercad and then I printed iteration 3 for each student and did another round of supply-swapping. They built another round of chargers and tested them.

Here’s iteration 3! It turned out pretty well.

I started printing iteration 3 as fast as I could, and I distributed these to the kids so they could make this year’s final version of the solar chargers. I am really pleased with how they’re turning out. I’ve gotten a few back, and they’re sturdy and high quality and work pretty well!

 

I even had one student that designed his own case that had an angled top, better for collecting sunlight in the winter. He laser-cut it at home, and it’s awesome. I did not take a picture of it yet, but I’ll do that soon. Maybe that’ll be iteration 4 or a separate branch of solar charger cases.

This is an amazing, fulfilling project. We are going to be donating the solar chargers to Homeward Alliance right after Memorial Day, so they can be distributed to people experiencing homelessness who need them. We expect we will have over 20 chargers to donate. We will also put a link to a survey on the chargers so our “clients” can give us feedback on how well they held up. The students really loved feeling like they were making a difference and experiencing what engineering really is.

If you’re interested in making these, I have posted a YouTube video with assembly instructions, and I’ll also share the parts lists and .stl files here.

Video:

 

Parts List: https://docs.google.com/spreadsheets/d/1X1u6yjNbjAu4dr34XgRzT953KN3b0fzujIJSVDwk_q8/edit#gid=0

Case .stl file: https://drive.google.com/file/d/1NDLWaPoC2yQwzlDsszhTPLA3drJ_VgZZ/view?usp=sharing

Lid .stl file: https://drive.google.com/file/d/1NtLVTKte3fTnh75H0FBPP34LZb973Js4/view?usp=sharing

 

 

Emergency Online Teaching – My Experience

I have not blogged in a while, and it’s hard to be reflective about your own work when you’re in the moment and so unsure WHAT you’re even doing, so you can’t pause to think about why or how. But now that I’ve finished my last day of teaching online content, I think it’s time to look back on what worked and what didn’t – because chances are, we’ll be doing this again before the coronavirus pandemic is over.

I live in Colorado, and as we watched the pandemic unfold on both coasts, we knew by early March that things were going to change for us drastically. We left for spring break on March 13th right after having a big open-house exhibition at my school, and after I attended my own daughters’ spring concerts and celebrations. When we left for spring break, we knew we weren’t coming back. Although our district had only planned for a 2-week break at the time, the writing was on the wall that we’d be out all quarter. We started to plan for it.

Our administrative team did a wonderful job creating a remote-learning plan that was flexible and could accommodate as many kids as possible.

• We did some test-runs with Zoom before spring break started, so teachers and students were familiar with the platform. We created a set of school norms for using Zoom and trained all of the students on these norms. Most teachers were able to run a class or two on Zoom, just as a trial, with kids spread out around the building and teachers conducting class from our office. We continued using Zoom for the duration of remote learning although we were aware of concerns with privacy. It really is a superior platform for online learning, and for a quarter, we decided to make the tradeoff.
• We extended our spring break an additional week, to give ourselves time to check computers out to students and write lesson plans. Students came to school early the week of March 23 to pick up their technology.
• We used Google Classroom as a central point for all remote learning. We agreed to use a standard structure, where assignments were labeled by day and week, and all assignments could be done asynchronously – with short video lessons where needed.
• We posted all assignments on Sunday evenings, with due dates a week later. (I found myself breaking from this slightly, however, posting Monday/Tuesday assignments on Sunday night and Thursday/Friday assignments on Wednesday).
• We agreed to hold online, live Zoom sessions twice a week for each class. Intensive classes (the core subjects) were held Monday/Friday, Venture classes (our project-based blocks) were held Tuesday/Thursday, and Wednesday was reserved for Advisory and staff meetings. We agreed the live sessions would not be required, but would be set up to provide support or teach the content live that was already accessible in the online videos.
• We kept a checklist of all of our students, so teachers could log which students were attending class and/or turning in work. The checklist was used to follow up with kids we didn’t hear from. The checklist was just a normal Google sheet that looked like an attendance roster, and next to each name there are checkboxes to log if we had seen/heard from the student. Through the checklist, we kept track of families dealing with Covid, families that needed food assistance, and some families that other obstacles to attending school – working, taking care of siblings, or lacking any internet except a phone data plan.

 

This is what my Google Classroom looked like, and every teacher in our school uses the same setup.

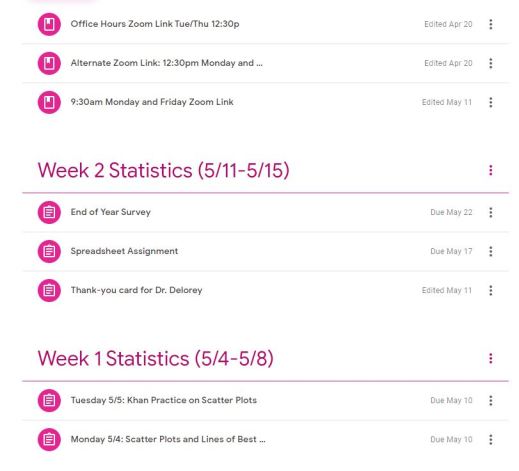
Zoom links are always posted at the top of the page. As you scroll down, weeks are in reverse-chronological order and all assignments are grouped under the week in which they were assigned. The consistency was helpful to everyone and I am so glad our admin just set the structure up for us.

I teach Algebra/Geometry (Integrated math, sort of), and had planned to teach quadratic functions, systems of equations, and data analysis. I had gotten a week into teaching quadratic functions when the semester ended, and I know my students that wanted to move on to Algebra II next year would need to know these topics. So I had to do the best I could teaching new content in this format. For each lesson, I made a video which I posted to YouTube, created some structured notes that went with the video, and then curated some Khan Academy exercises for practice. I assigned 1-3 practice sets for each lesson, so it wasn’t an overwhelming amount of work. If we had been in the classroom, the structured notes would have been set up as group activities – I just adapted them to be individual notes instead.

I think a huge part of the value of the video is for the students to connect with me by hearing my voice and seeing my face, so the videos are probably not as meaningful for you. I know there are tons of videos out there that teach the exact same content I’m teaching – but I made these anyway, because I believe there’s value in the students hearing directly from me and knowing I care and believe in them. You can use them if you like, but I really do think your students benefit from videos you make yourself too.

Quadratic Functions Playlist

Systems of Equations Playlist

Statistics Playlist

Each day, I asked the students to do the Khan Academy exercises, mark the assignment as “done” in Google Classroom, and write a short reflection on how it went. For the units on Quadratics and Systems, I included a small end-of-unit assessment. For the Quadratics unit, it was a packet of problems I curated from an SAT test prep book. For the Systems unit, I assigned the students a computer programming project as an assessment.

Our grading system is a competency-based system, with marks of “Not yet”, “Basic Understanding”, and “Exemplary Understanding” for content. There really is not a good and fair way to check students’ competency levels in this kind of system. So if a student did most of the assignments and put in a solid effort on the assessment with reasoning I could understand, I gave him or her a mark of “Basic Understanding”. A few standout students received marks of Exemplary Understanding, but I reserved this for when I could tell it was really warranted. When in doubt, I used the “Basic” mark. If students did not participate at all and did not do assignments, I left the grade blank as if they didn’t take the class. They’ll get a chance to learn it in the future when learning is purposeful and planned, not emergency.

So that’s what I decided to do. Here are my reflections on how it went.

From my perspective – I felt like this was a decent first attempt at online teaching. I actually do like Khan Academy as a resource for practice problems. The students can get feedback right away, they can use the hints and videos, and I could screen-share with students during my office hours to help them with the practice. It was super useful. I probably will use Khan’s exercise sets next year when we have to go remote again. A little more than half of my students completed work regularly. About a third showed up consistently to our synchronous Zoom sessions. I enjoyed the online zoom sessions, and after I got about a month into the schedule, I really liked it. I did do some repetitive work – creating the videos and resources for the lesson, and then teaching the exact same lesson live twice, then teaching it again during office hours – but my days were so much more flexible and easy to manage. I had to carve out a couple of hours for online classes each day and then I could finish the rest of the work on my own time. At 3pm or 2am or whenever it was a good time for me. By the time May rolled around, I was very comfortable managing my time this way, taking care of my house and family and balancing the school needs. And really, I’m far less stressed right now than I usually am in May. MUCH less stressed. I’m kind of thriving on this flexible online schedule. I get outside a little every day, tinker and create, play with the pets, make a variety of food, and enjoy spending time with my husband and kids. I was really sad and stressed when the quarter started, but now that it’s mid-May I’m doing pretty well.

From the kids’ perspective, it’s more complicated. I gave an end-of-year survey to my students today and was surprised at some of the results. The first question was about student motivation levels. Less than half of my students responded to the survey, so the results may yet change if I get more.

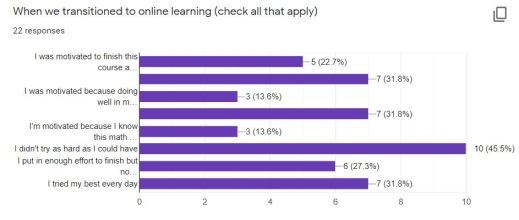
The bars correspond to these prompts:

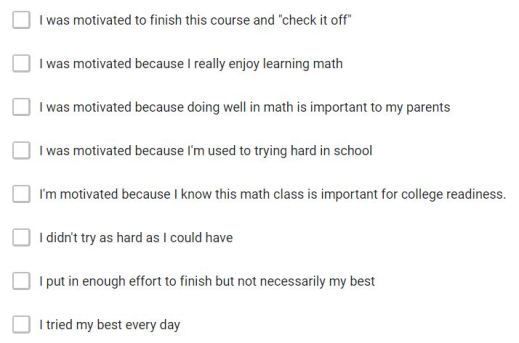
Students could check multiple boxes. The most popular answer was: “I didn’t try as hard as I could have”. Second most popular was a three-way tie: I was motivated because I really enjoy math, I was motivated because I’m used to trying hard in school, and I tried my best every day. It seems, though, a majority of students are disappointed in their effort.

 

I asked students what they thought of Khan Academy as a practice tool. This surprised me.

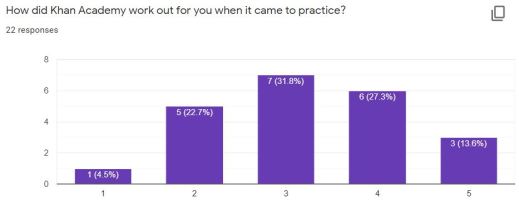
1 corresponds with “It’s terrible, please don’t use it anymore” and 5 corresponds with “It’s a good way to practice and you should use it next year too”. Generally students are OK with Khan as a practice tool. They don’t love it but don’t hate it. Some helpful comments included “It’s good for practice, but I don’t learn new content well from it”, “I like that I know right away if I got it right and can get help if not”, and “It was only a few questions so it wasn’t overwhelming.”

 

I asked the students how they felt about the feedback they got during online learning, with 1 being “Not Nearly Enough Feedback” and 5 being “I am satisfied with the feedback I got”.

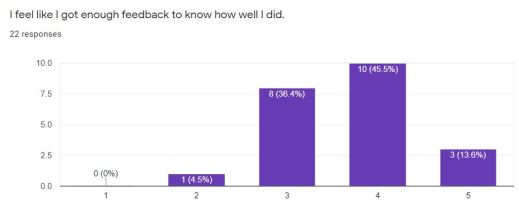
I almost did a spit-take because I got REALLY behind on grading – not just summative assessments and comments, but the daily work of doing into Google Classroom and just checking off assignments and writing “Good job”. I certainly didn’t give them this feedback, unless they asked for it in office hours or zoom sessions. Strange perception. I expected them to rake me over the coals and hold me accountable for getting behind on feedback. I don’t know why they didn’t. Maybe because they practiced on Khan they knew what progress they were making? Maybe because I sent emails reminding them about stuff?

 

I asked students if they felt ready to move on to the next math class. This graph also surprised me.

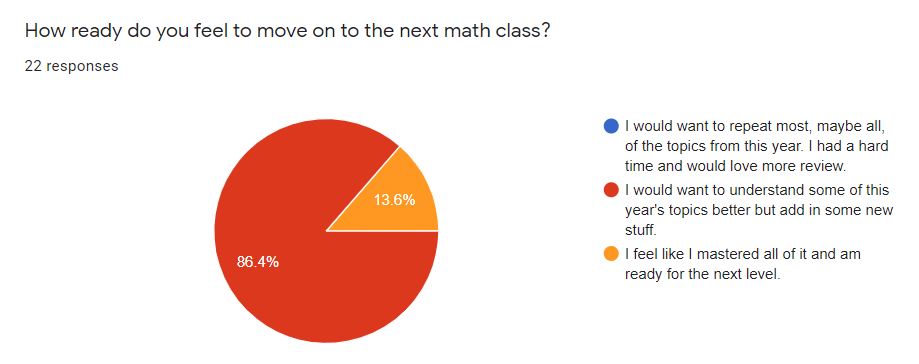
A vast majority of the students wants some review and some new stuff next year. Huh. I would say the kids in the “I feel like I mastered it” category are also the ones I would have pegged as fully ready to move on, but some of the other kids in the 86% are ready but don’t perceive themselves as ready.

 

I asked students what topics they’re interested in learning more about when it comes to math. This is what they said.

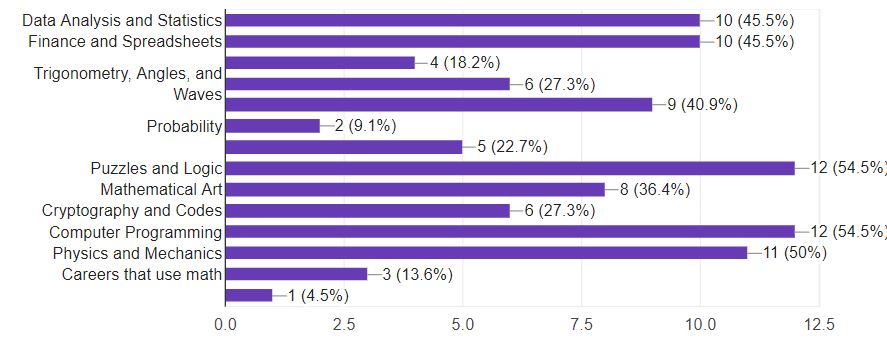
Some of the labels disappeared so this is a list of the choices.

The most popular answers were: Puzzles and Logic, Computer Programming, Physics and Mechanics, Data Analysis and Statistics, Finance and Spreadsheets, and Measurement/Design/Engineering/Construction. The least popular were: Advanced Functions/Polynomials/Calculus, Probability, Solving more and more difficult equations, and careers that use math.

I brought this question up just in case standardized testing gets postponed, cancelled, or has a lower priority placed on it, maybe freeing up a little more math time for the things kids would like to learn. We do SO much with functions in high school math. It’s a bit much, in my opinion, when there’s so much math out there that kids like.

I asked one final question which was: If math is online again next year, what do you think you need to be successful? The responses were all over the map, some hopeful, some disappointed. They’re important to read. There are a lot of kids beating themselves up for not feeling more motivated and I think they’re being a little hard on themselves, considering.

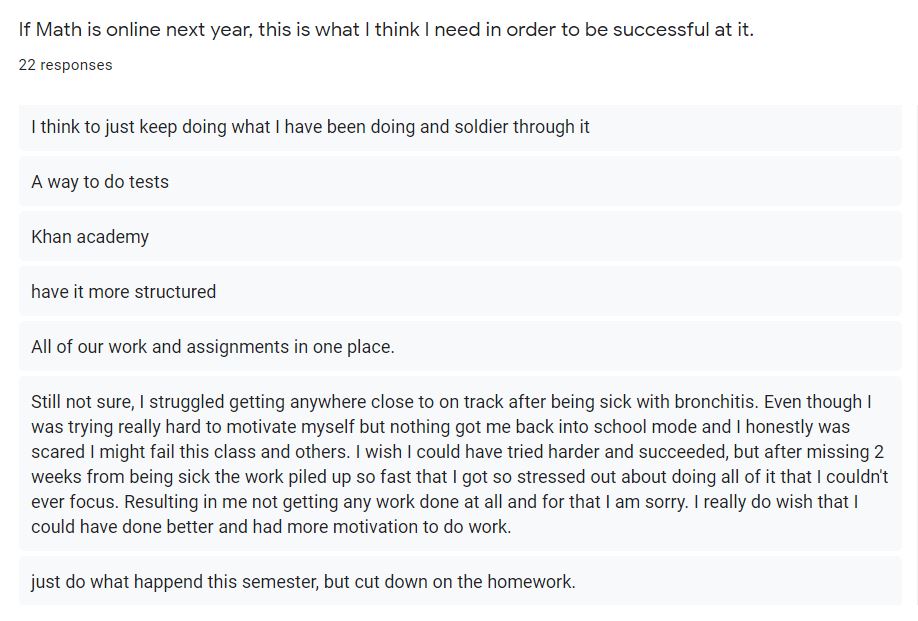
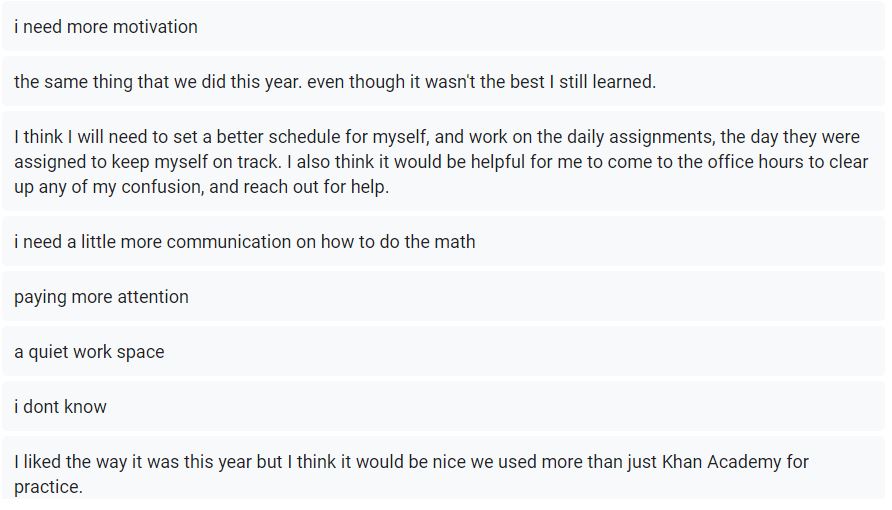
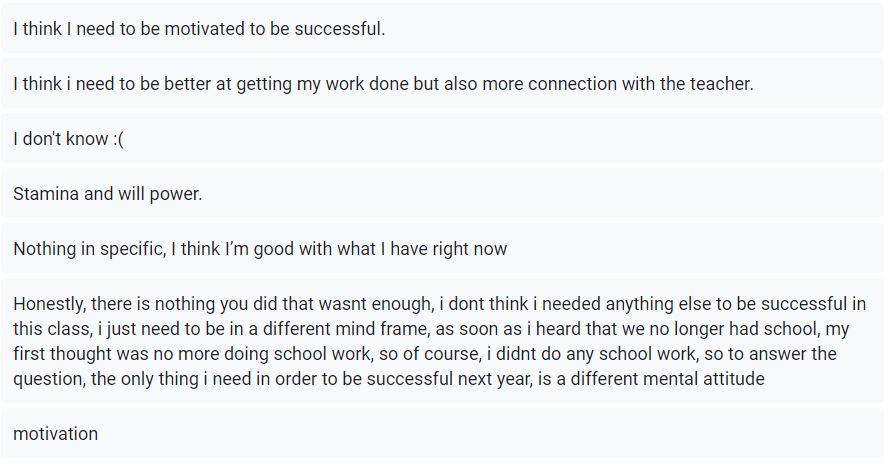
So there it is, my first emergency-remote-learning quarter of Algebra in the bag. Lots to think about as we head into next fall and have to continue keeping kids safe and somehow figuring out how to help them learn.

How did it go for you? What would you do differently and what did you like about your system?

 

 

 

 

 

Perpendicular Lines and Coding a Tartan

Linear functions are at the heart of 8th grade math and Algebra I, and I enjoy finding those ways we engage with functions in real-life situations… including creative coding!

As we learn about slope, it’s an interesting challenge for students to explore what kind of line would be perpendicular to a given line, and I like to use that challenge to deepen their understanding of what slope is. We start with some lines and without showing them how, I challenge them to find a line that makes a perfect 90 degree angle to the given line.

Perpendicular Slope Worksheet

We have a discussion about when this understanding would be important. Architects or designers might use the concept, for example, if they have to design right-angles that are not perfectly aligned to their grid. Video-game designers may use the concept if a shooter is facing an enemy, and you have to strafe at 90 degrees from the angle you expect their projectile to come from.

Or, you might use the idea of perpendicular lines to just make pretty art, which is what we did with this mini-project.

I reminded the students about Tartans and how groups in Scotland use a Tartan as part of their identity – whether region, occupation, clan, or something else.
https://www.scotlandshop.com/us/tartan-finder

My family and I hiked in Scotland this past summer and noticed tartans of the MacDonald and Campbell clans everywhere!

For math projects, I’ve written before about how much I like coding in Khan Academy’s Javascript interface, so here’s the pitch again: it’s great for mini-projects. It’s easy to push a sample project out to students, easy to debug and run, fun and engaging to color and animate, easy to save and share as long as you have a KA account.

We start by going over how to color the background and stroke and fill colors, and how to place points on the coordinate grid. We first discuss where (0,0) might be and then discover together it’s in the upper left (!) and I challenge students to place points in all four corners and in the center. This is what they end up with.

Coordinates Program

Then we add in the draw() loop and get the points moving.

Coordinates Program animated

That’s day 1. On day 2, we can introduce the project. Students have to make a personalized, unique Tartan with colors and stripe widths they choose. The tartan must have at least 8 lines on a colorful background. The lines must be perpendicular, but can’t be perfectly horizontal or vertical, or at a 45 degree angle. Lines must start at an edge.

It gives some interesting challenges as students figure out what coordinates would start a line at the edge they want, and then how to create slopes that are perpendicular. In an example video, I show how a slope of +4 in the x direction and +5 in the y direction is exactly perpendicular to a slope of -4 in the y direction and +5 in the x direction. Make one value negative, and swap x and y.
Perpendicular Lines video

My last class made some very nice tartans.

Bryson’s Tartan

Tessa’s Tartan

It’s a quick, 2 or 3 day mini project that gives students some context for slopes and intercepts and allows them to get a little creative.

Enjoy!